Acquisition Parameters
- \(\delta\): pulse duration
- \(\Delta\): time separation between the two diffusion gradients
- \(G\): gradient strength
- \(\mathbf{n}\): gradient direction
- TE: echo time
Diffusion-sensitizing gradients
A diffusion-sensitizing magnetic field gradient can be characterized by a so-called q-vector \(\mathbf{q}\) in q-space is defined as:
\[ \mathbf{q} = \frac{\gamma \delta}{2 \pi} \mathbf{g} = \frac{\gamma \delta G}{2\pi} \mathbf{n}, \]where \(\gamma\) is the gyromagnetic ratio, \(\delta\) is the gradient pulse duration, \(\mathbf{g}\) is the diffusion-sensitizing gradient and \(G = \| \mathbf{g} \|\) is its norm. The direction of the q-vector is given by the unit vector \(\mathbf{n} = \mathbf{g} / \| \mathbf{g} \|\). The b-value is then defined as:
\[ b = \gamma^2 \delta^2 G^2 (\Delta - \delta/3), \] according to the Stejskal-Tanner equation (Stejskal and Tanner 1965), where \(\Delta\) is the diffusion time, which leads to:
\[ \mathbf{q} = \| \mathbf{q} \| \mathbf{n} = \frac{\gamma \delta G}{2 \pi} \mathbf{n} = \frac{1}{2 \pi} \sqrt{\frac{b}{\Delta - \delta / 3}} \mathbf{n}. \]The application of a diffusion-sensitizing gradient leads to an MR signal decay \(E(\mathbf{q})\) with respect to the \(T_2\)-weighted signal in the absence of diffusion gradients.
Tissue Microstructure
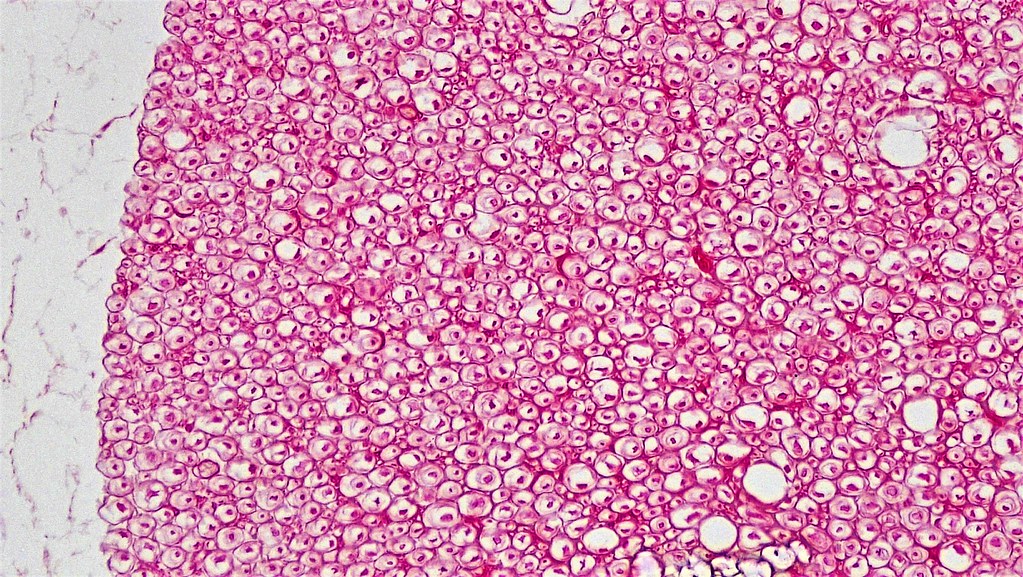
Taken from https://www.flickr.com/photos/146824358@N03/40106759090/in/album-72157666241437517/.
- Axon diameter: it is of the order of \(1\mu m\)
- Axonal density: both intra- and extra-axonal spaces exist
- Number of axons: it depends on the voxel size
- Orientation dispersion: axons are not perfectly aligned
Tissue Model
Model \(\mathcal{M}\) with the following parameters:
- \(\mathbf{u}\): cylinder axis mean;
- \(\kappa\): cylinder axis concentration (can be set to \(\infty\) to model parallel cylinders);
- \(R\): cylinder radius mean;
- \(\sigma_R\): cylinder radius standard deviation (can be set to \(0\) to model constant radius cylinders);
- \(f_r\): cylinder density;
- \(D_0\): intra-axonal intrinsic diffusivity within the cylinder;
- \(\lambda_\parallel\): extra-axonal parallel diffusivity along the cylinder axis;
- \(\lambda_\perp\): extra-axonal perpendicular diffusivity to the cylinder axis;
- \(n_c\): number of cylinders (determined by voxel size and axonal density).
MR Signal
In an anisotropic medium with main direction \(\mathbf{u}\), we can decompose gradient direction \(\mathbf{n}\) as a direct sum of its projection along the main direction \(\mathbf{u}\) and its projection \(\mathbf{n}_\perp\) in the perpendicular plane to that direction:
\[ \mathbf{n} = \langle \mathbf{n}, \mathbf{u} \rangle \mathbf{u} \oplus \left( \mathbf{n} - \langle \mathbf{n}, \mathbf{u} \rangle \mathbf{u} \right) = \mathbf{n}_\parallel \oplus \mathbf{n}_\perp, \]which lets us define
\[ \mathbf{q} = \frac{\gamma \delta G}{2 \pi} (\mathbf{n}_\parallel \oplus \mathbf{n}_\perp) = \mathbf{q}_\parallel \oplus \mathbf{q}_\perp. \] Since: \[ \| \mathbf{n}_\parallel \|^2 = \langle \mathbf{n}, \mathbf{u} \rangle^2, \quad \| \mathbf{n}_\perp \|^2 = \sqrt{1- \langle \mathbf{n}, \mathbf{u} \rangle^2}, \]we have:
\[ \| \mathbf{q}_\parallel \|^2 = \frac{\gamma^2 \delta^2 G^2}{4 \pi^2} \langle \mathbf{n}, \mathbf{u} \rangle^2, \quad \| \mathbf{q}_\perp \|^2 = \frac{\gamma^2 \delta^2 G^2}{4 \pi^2} \left(1 - \langle \mathbf{n}, \mathbf{u} \rangle^2 \right). \]The MR signal decay \(E(\mathbf{q}; \mathcal{M})\) depends on the geometry of the tissue in which diffusion occur through model \(\mathcal{M}\) and can be decomposed as:
\[ E(\mathbf{q}; \mathcal{M}) = E(\mathbf{q}_\parallel; \mathcal{M}) E(\mathbf{q}_\perp; \mathcal{M}), \]where \(E(\mathbf{q}_\parallel)\) and \(E(\mathbf{q}_\perp)\) are the MR signal decays induced by diffusion parallel and perpendicular to the cylinder axis, respectively.
The MR signal decay induces by diffusion parallel to the cylinder axis is usually modeled as a mono-exponential decay induced by 1D Gaussian diffusion:
\[ E(\mathbf{q}_\parallel; \mathcal{M}) = \exp(-b D_0 \langle \mathbf{n}, \mathbf{u} \rangle^2). \]Overview
Models that rely on an approximate solution of the Bloch-Torrey equation for magnetization with diffusion-induced magnetization transfer under the narrow pulse approximation (NPA):
- Söderman’s model (Söderman and Jönsson 1995);
- Callaghan’s model (Callaghan 1995).
Models that rely on the Gaussian phase approximation (GPA), i.e. that diffusion remains Gaussian but with apparent diffusion coefficient that depends on the cylinder’s radius:
- Neuman’s model (Neuman 1974);
- Van Gelderen’s model (Vangelderen et al. 1994).
Models that rely on the geometric simplification of diffusion between two parallel planes under the NPA:
- Stanisz’s model (Stanisz et al. 1997).
Stanisz’s model
Neuman (1974) and Vangelderen et al. (1994) model the diffusion in the perpendicular plane to the cylinder axis as a two-dimensional zero-mean Gaussian distribution with variance \(2 D_\perp^\text{app} \tau\) where \(D_\perp^\text{app}\) is the apparent radial diffusivity in the intra-axonal space and is defined as a function of the cylinder radius \(R\).
Stanisz et al. (1997) take on a different approach and provide models for the restricted diffusion in cylindrical and spherical geometries. As such, it is useful to model both isotropic restricted diffusion in glial cells and anisotropic restricted diffusion in axons. This is achieved by using in both cases a simple one-dimensional model of restricted diffusion within infinite parallel membranes. This assumption is validated by comparing the signal loss with respect to the model proposed by Neuman (1974). Accordingly, they use the model of signal attenuation induced by water diffusing between flat, impermeable barriers of spacing \(\ell\) proposed in Tanner (1978):
\[ \begin{aligned} & S_\perp^\mathrm{Stanisz}(\delta, \Delta, G; \ell, D_0) = 2 \frac{1 - \cos (\gamma \delta G \ell)}{(\gamma \delta G \ell)^2} \\ &+ 4 (\gamma \delta G \ell)^2 \sum_{n=1}^\infty e^{-n^2 \pi^2 D_0 \Delta / \ell^2} \frac{1 - (-1)^n \cos (\gamma \delta G \ell)}{((\gamma \delta G \ell)^2 - (n \pi)^2)^2}. \end{aligned} \]One gets restricted diffusion in a cylinder or in a sphere by setting \(\ell\) to the corresponding radius \(R\). The signal in this model is not a mono-exponential decay and therefore the resulting density of water molecule displacements is not a Gaussian distribution, which is probably a more realistic assumption for water diffusing in a trapped environment. The model however relies on the short pulse duration (SPD) approximation. In the case of restricted diffusion within a cylinder, the diffusion gradient strength \(G\) should also be replaced by \(G \sqrt{1 - \braket{\mathbf{n}, \mathbf{u}}^2}\), where \(\mathbf{u}\) is the cylinder axis.
Neuman’s model
Neuman (1974) assumes Gaussian diffusion during the gradient pulse and that:
\[ \delta \sim \Delta, \]Under these assumptions, Neuman (1974) predicts that the signal attenuation induced by diffusion perpendicular to the cylinder axis reads:
\[ S_\perp^\mathrm{Neuman}(\delta, G, \mathbf{n}, \mathrm{TE}; \mathbf{u}, R, D_0) = e^{ -\frac{7 \gamma^2 \delta^2 G^2 R^4}{48 D_0 \mathrm{TE}} \left( 1 - \braket{\mathbf{n}, \mathbf{u}}^2 \right) \left( 2 - \frac{99 R^2}{56 D_0 \mathrm{TE}} \right) }, \]where \(\mathrm{TE}\) is the echo time. Note that, similarly to Soderman’s model, the signal attenuation induced by diffusion perpendicular to the cylinder axis under Neuman’s model is independent from the diffusion time \(\Delta\). However, in contrast to Soderman’s model, the signal depends on the echo time \(\mathrm{TE}\) and the free diffusion coefficient \(D_0\).
Additional assumption required
The term
\[ 2 - \frac{99 R^2}{56 D_0 \mathrm{TE}} \]can be negative, leading to non-physical (\(\ge 1\)) signal attenuation values. Therefore, Neuman’s model is not valid for all parameter values. In particular, it is only valid for:
\[ \frac{99 R^2}{56 D_0 \mathrm{TE}} \le 2 \Leftrightarrow \mathrm{TE} \ge \frac{99 R^2}{112 D_0}. \]Söderman’s model
Söderman and Jönsson (1995) assumes that the pulse duration \(\delta\) is small enough to neglect the diffusion during the pulse and that the diffusion time \(\Delta\) is long enough to make diffusion restricted within a cylinder of radius \(R\) and free diffusion coefficient \(D_0\). In other terms, they assume that:
\[ \delta \to 0 \quad \text{and} \quad \Delta \gg R^2 / D_0. \]Under these assumptions, Söderman and Jönsson (1995) predicts that the signal attenuation induced by diffusion perpendicular to the cylinder axis reads:
\[ S_\perp^\mathrm{Soderman}(\delta, G, \mathbf{n}; \mathbf{u}, R) = \left( 2 \frac{J_1(\gamma \delta G \sqrt{1 - \braket{\mathbf{n}, \mathbf{u}}^2} R)}{\gamma \delta G \sqrt{1 - \braket{\mathbf{n}, \mathbf{u}}^2} R} \right)^2, \]where \(J_1\) is the Bessel function of the first kind of order \(1\). Note that the signal attenuation induced by diffusion perpendicular to the cylinder axis is independent from the diffusion time \(\Delta\) and the free diffusion coefficient \(D_0\).
Van Gelderen’s model
Vangelderen et al. (1994) make no assumptions on the acquisition sequence and the gradient waveform. They assume Gaussian diffusion during the gradient pulse.
Under these assumptions, Vangelderen et al. (1994) predicts that the signal attenuation induced by diffusion perpendicular to the cylinder axis reads:
\[ \begin{aligned} & \log S_\perp^\mathrm{VanGelderen}(\delta, \Delta, G, \mathbf{n}; \mathbf{u}, R, D_0) = -2 \gamma^2 G^2 \left( 1 - \braket{\mathbf{n}, \mathbf{u}}^2 \right) \\ &\cdot \sum_{m=1}^\infty \frac{2 D_0 \alpha_m^2 \delta - 2 + 2 e^{-D_0 \alpha_m^2 \delta} + 2 e^{-D_0 \alpha_m^2 \Delta} - e^{-D_0 \alpha_m^2 (\Delta - \delta)} - e^{-D_0 \alpha_m^2 (\Delta + \delta)}}{D_0^2 \alpha_m^6 \left( R^2 \alpha_m^2 - 1 \right)}, \end{aligned} \]where \(\alpha_m\) are the roots of the equation:
\[ J_1^\prime(\alpha_m R) = 0. \]Callaghan’s model
Callaghan (1995) relaxes the assumption that \(\Delta \gg \frac{R^2}{D_0}\). It still assumes that:
\[ \delta \to 0. \]Under these assumptions, Callaghan (1995) predicts that the signal attenuation induced by diffusion perpendicular to the cylinder axis reads:
\[ \begin{aligned} & S_\perp^\mathrm{Callaghan}(\delta, \Delta, G, \mathbf{n}; \mathbf{u}, R, D_0) = 4 \sum_{n = 0}^\infty 2^{n > 0} \sum_{m=1}^\infty e^{-\beta_{nm}^2 \frac{D_0 \Delta}{R^2}} \\ &\cdot \frac{\beta_{nm}^2}{\beta_{nm}^2 - n^2} \left( \frac{\left(\gamma \delta G \sqrt{1 - \braket{\mathbf{n}, \mathbf{u}}^2} R\right) J_n^\prime \left(\gamma \delta G \sqrt{1 - \braket{\mathbf{n}, \mathbf{u}}^2} R \right)}{\left(\gamma \delta G \sqrt{1 - \braket{\mathbf{n}, \mathbf{u}}^2} R\right)^2 - \beta_{nm}^2} \right)^2 \end{aligned} \]where \(J_n^\prime\) is the derivative of the Bessel function of the first kind of order \(n\) and \(\beta_{nm}\) are the non-negative arguments at which \(J_n^\prime\) equals zero or equivalently, at which \(J_n\) has a local extremum:
\[ J_n^\prime(\beta_{nm}) = 0. \]Model
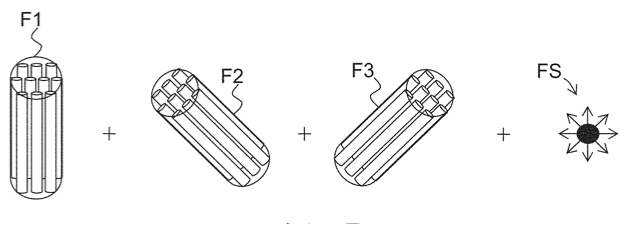
\[
E(\mathbf{q}) = \sum_{j=1}^M f_r^{(j)} E_r(\mathbf{q}; \mathbf{u}_j) + f_h E_h(\mathbf{q}) + f_\mathrm{csf} E_\mathrm{csf}(\mathbf{q}),
\]
with:
- \(E_r(\mathbf{q}; \mathbf{u}_j)\): the signal attenuation induced by restricted diffusion in an axon bundle with mean orientation \(\mathbf{u}_j\) according to previous theory (4 free parameters);
- \(E_h(\mathbf{q})\): the signal attenuation induced by hindered diffusion in the extra-axonal space modeled as diffusion tensor model \(E_h(\mathbf{q}) = e^{-\mathbf{q}^T \mathbf{D}_h \mathbf{q}}\) (6 free parameters);
- \(E_\mathrm{csf}(\mathbf{q})\): the signal attenuation induced by free diffusion in the CSF, i.e. \(E_\mathrm{csf}(\mathbf{q}) = e^{-D_\mathrm{csf} \|q\|^2}\) (1 free parameter).
Axonal density and axon diameter
Models have focus either on the axonal density or the axon diameter:
- Axon density: CHARMED (Assaf and Basser 2005);
- Axon diameter: AxCaliber (Assaf et al. 2008; Barazany, Basser, and Assaf 2009).
Axon diameter estimation requires acquisitions with multiple diffusion times (\(\Delta\));
The estimation of both axonal density and axon diameter is improved if time dependence of the extra-axonal apparent radial diffusivity is taken into account (Burcaw, Fieremans, and Novikov 2015; De Santis, Jones, and Roebroeck 2016).
CHARMED
- \(f_\mathrm{csf} = 0\);
- \(M\) up to \(2\);
- Fixed distribution of axonal radii: \(\{(1.5, 0.0212), (2.5, 0.1072), (3.5, 0.1944), (4.5, 0.2667), (5.5, 0.2150), (6.5, 0.1956) \}\);
- Neuman’s model for restricted diffusion in cylinders.
Proton gyromagnetic ratio
\(\gamma = 267.5 \, rad/ms/mT\)
Maximal gradient strength
\(40 - 400 \, mT/m\)
Diffusion time
\(10 - 100 \, ms\)
Pulse duration
\(1 - 40 \, ms\)
Intra-axonal free diffusion coefficient (at \(37^\circ C\))
\(2 - 3 \mu m^2/ms\)
http://dtrx.de/od/diff/, Pizzolato et al. (2023)Extra-axonal apparent radial diffusivity
\(0.1 - 0.6 \mu m^2/ms\)
(Szafer, Zhong, and Gore 1995; Burcaw, Fieremans, and Novikov 2015)Voxel size
1 - 2 mm
References
Aboitiz, Francisco, Arnold B Scheibel, Robin S Fisher, and Eran Zaidel. 1992. “Fiber Composition of the Human Corpus Callosum.” Brain Research 598 (1-2): 143–53.
Alexander, Daniel C. 2008. “A General Framework for Experiment Design in Diffusion MRI and Its Application in Measuring Direct Tissue-Microstructure Features.” Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 60 (2): 439–48.
Assaf, Yaniv, and Peter J Basser. 2005. “Composite Hindered and Restricted Model of Diffusion (CHARMED) MR Imaging of the Human Brain.” Neuroimage 27 (1): 48–58.
Assaf, Yaniv, Tamar Blumenfeld-Katzir, Yossi Yovel, and Peter J Basser. 2008. “AxCaliber: A Method for Measuring Axon Diameter Distribution from Diffusion MRI.” Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 59 (6): 1347–54.
Barazany, Daniel, Peter J Basser, and Yaniv Assaf. 2009. “In Vivo Measurement of Axon Diameter Distribution in the Corpus Callosum of Rat Brain.” Brain 132 (5): 1210–20.
Burcaw, Lauren M, Els Fieremans, and Dmitry S Novikov. 2015. “Mesoscopic Structure of Neuronal Tracts from Time-Dependent Diffusion.” NeuroImage 114: 18–37.
Callaghan, Paul T. 1995. “Pulsed-Gradient Spin-Echo NMR for Planar, Cylindrical, and Spherical Pores Under Conditions of Wall Relaxation.” Journal of Magnetic Resonance, Series A 113 (1): 53–59.
De Santis, Silvia, Derek K Jones, and Alard Roebroeck. 2016. “Including Diffusion Time Dependence in the Extra-Axonal Space Improves in Vivo Estimates of Axonal Diameter and Density in Human White Matter.” NeuroImage 130: 91–103.
Ferizi, Uran, Torben Schneider, Thomas Witzel, Lawrence L Wald, Hui Zhang, Claudia AM Wheeler-Kingshott, and Daniel C Alexander. 2015. “White Matter Compartment Models for in Vivo Diffusion MRI at 300 mT/m.” NeuroImage 118: 468–83.
Huang, Susie Y, Aapo Nummenmaa, Thomas Witzel, Tanguy Duval, Julien Cohen-Adad, Lawrence L Wald, and Jennifer A McNab. 2015. “The Impact of Gradient Strength on in Vivo Diffusion MRI Estimates of Axon Diameter.” Neuroimage 106: 464–72.
Neuman, CH. 1974. “Spin Echo of Spins Diffusing in a Bounded Medium.” The Journal of Chemical Physics 60 (11): 4508–11. https://doi.org/10.1063/1.1680931.
Pizzolato, Marco, Erick Jorge Canales-Rodrı́guez, Mariam Andersson, and Tim B Dyrby. 2023. “Axial and Radial Axonal Diffusivities and Radii from Single Encoding Strongly Diffusion-Weighted MRI.” Medical Image Analysis 86: 102767.
Söderman, Olle, and Bengt Jönsson. 1995. “Restricted Diffusion in Cylindrical Geometry.” Journal of Magnetic Resonance, Series A 117 (1): 94–97.
Stanisz, Greg J, Graham A Wright, R Mark Henkelman, and Aaron Szafer. 1997. “An Analytical Model of Restricted Diffusion in Bovine Optic Nerve.” Magnetic Resonance in Medicine 37 (1): 103–11. https://doi.org/10.1002/mrm.1910370115.
Stejskal, Edward O, and John E Tanner. 1965. “Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient.” The Journal of Chemical Physics 42 (1): 288–92. https://doi.org/10.1063/1.1695690.
Szafer, Aaron, Jianhui Zhong, and John C Gore. 1995. “Theoretical Model for Water Diffusion in Tissues.” Magnetic Resonance in Medicine 33 (5): 697–712.
Tanner, John E. 1978. “Transient Diffusion in a System Partitioned by Permeable Barriers. Application to NMR Measurements with a Pulsed Field Gradient.” The Journal of Chemical Physics 69 (4): 1748–54. https://doi.org/10.1063/1.436751.
Vangelderen, P, D DesPres, PCM Vanzijl, and CTW Moonen. 1994. “Evaluation of Restricted Diffusion in Cylinders. Phosphocreatine in Rabbit Leg Muscle.” Journal of Magnetic Resonance, Series B 103 (3): 255–60. https://doi.org/10.1006/jmrb.1994.1038.
